Fermi 粒子加速—科普介绍  精选
精选
||
Fermi (费米)加速是费米为解释高能宇宙线的形成机理而提出的一种粒子加速机制,目前已经在天体物理、
空间物理和等离子体物理中得到了广泛的应用。(维基百科:http://en.wikipedia.org/wiki/Fermi_acceleration)
下面只是非常简单地用文字描述一下有关物理过程。
1. Fermi加速基本原理 (Basic principles)
相向运动的磁镜系统中,粒子可以得到加速。根据等离子体物理中的纵向不变量(longitudinal invariant:平行速度与力线长度之积为常数),很容易理解这一基本的加速机制(即相向运动导致磁力线变短、粒子平行速度增加)。当然,泛泛而言,无碰撞等离子体中粒子加速都是要靠电场来实现的;磁场只改变速度方向,不改变速度大小。因此,粒子加速归根究底都是电场引起的。关键要分清,电场的来源和存在形式(如等离子体切割磁力线运动、磁场随时间的变化等都可产生电场),如何与粒子发生作用等。
一般教科书中提及Fermi加速时,通常假设速度为V的粒子与速度为U的散射元(SC:scattering center)之间发生弹性碰撞,即如果SC静止不动,则粒子(质量m)反弹前后的速度大小相同,方向相反,由V+U变为-(V+U)。则实验室坐标系中,粒子碰撞前后的速度大小分别为:V 和|-(V+U)-U|,故在实验室坐标系中,粒子动能变化为 2m(U^2-V.U), 其中.表示速度矢量内积。当,(1) SC与粒子同向运动时,内积项贡献为负,但平方项贡献为正,粒子是否损失能量取决于两项的相对大小;(2)不同向时,则动能变化项中两项皆为正,故粒子能量总是增加。这是实验室坐标系下的结论,在SC坐标系中,粒子速度/动能不变,即没有加速。这说明,加/减速完全是由于SC的运动造成的。可知当U=0时,无速度变化。请思考,加速所需要的电场是如何产生的。
常用的一个比喻就是,打乒乓球,粒子比喻成球,散射元为球拍。运动球拍可使球加速,能量增加。(Like a ping-pong ball caught between two converging paddles)
2. 一阶与二阶Fermi加速(Fist-order and second-order Fermi Acceleration)
一般研究粒子加速时,粒子能量大都已经远快于SC的运动速度(U=o(V)),故动能变化除以粒子能量,得到的是二阶小项与一阶小项之和。这也说明,一般Fermi机制起作用时,每次的粒子能量变化都是小项;欲获得显著的加速,必须进行反复的Fermi加速。当一阶项起主导作用时,则称为一阶Fermi 加速;当某些情况下,所有起加速和减速作用的一阶项平均掉之后,则只余下二阶项,此时就称为二阶Fermi加速。
3. 迎头碰与追尾碰(head-on collisions and rear-on(tail-on) collisions)
SC与粒子相向运动,就是head-on collision; 反之,为tail-on collision. 后者之所以能发生,正是因为一般粒子速度更快一些。考虑到能量变化中的平方项一般较小,所以通常情况下,可以说head-on collisions中粒子得到能量,而在tail-on collisions 中粒子失去能量。如果,一个Fermi加速系统中,发生的head-on collisions的数目与tail-on collisions的数目相当(强度也差不多),则一阶项就相互抵消了,仅就余下二阶项了,为二阶Fermi加速。如果head-on占主导, 则为一阶Fermi加速。
4. Stochastic acceleration或二阶Fermi加速:可见,很奇怪的一件事就是,迎头碰和追尾碰相当时,仍存在二阶Fermi加速。这种加速一般发生于SC是随机分布的湍动元的情况。此时每个湍动元就是一个SC, 速度可以构成对称的类高斯分布,整体上可以不动,这时与一束粒子发生作用,迎头碰和追尾碰总效果相当,故一阶项消失,二阶项由于是每个SC的速度平方项的总和,则存留下来,粒子整体上就得到了加速。这称为随机加速:stochastic acceleration, 是一种二阶Fermi加速。
5. 一阶Fermi加速:
在相向运动的磁镜系统中,粒子每次返回都是发生的迎头碰(实验室坐标系下观察),故粒子不断被加速,为一阶Fermi加速。重联后出流区中快速回缩的力线上的粒子的加速(可反弹的原因是远处力线和湍动所构成的类磁镜效应)也全是head-on collisions, 故是一阶Fermi accelearation.
6. 平行激波加速DSA (diffusive shock acceleration):一阶Fermi加速
平行激波加速系统是让人费解的一种打ping-pong的一阶Fermi加速过程。为理解好基本物理图像,有几个基本假设:(1)上下游高度湍动,湍动元大体被所在的上下游等离子体携带着一起运动;(2)无论在上游还是下游,由于与湍流元的相互作用,粒子一旦进入上下游后就立刻被散射成各向同性分布,而且所得到的各向同性的分布是在所在的流体静止坐标系中观测得到的。
可以任意选择坐标系来分析,分析正确的话肯定会得到相同的物理后果。为方便,我们以激波坐标系为例,上游速度超声速、下游亚声速,上游比下游快 delta_U = U_up – U_down, 激波坐标系中,上下游速度是同向的。物理图像如下面三图所示。至于上下游湍流\波动的产生,是一个关于粒子激发波动的等离子体不稳定性的问题;这里只讨论系统经历最初的波动增长而达到一种稳态时的情况。波的激发恐需专文描述。
平行激波的波面上磁场没有变化,因此,平行激波波面主要是流体结构,上游流体流至下游被加速和压缩;系统中的高能粒子是无碰撞的,激波面对于这些高能粒子成份而言没有任何作用(磁场不变),所以粒子可以轻易穿越波阵面;另一方面,不论是处于上游还是下游的粒子,都是被其中的湍动元裹挟着前行,能量虽高,但苦于无法冲破湍动的阻碍,故始终存在于上下游,随上下游湍流元一起整体运动(频繁的碰撞阻止了粒子的逃逸)。所以,上下游其实都可看成两种成份构成,一是流体,一是高能粒子。分别在上下游静止坐标系中,看到的粒子速度都是同心圆(各向同性分布,见图3中的速度分布图,以上下游速度为圆心的同心圆(速度空间中绘图)、或者高斯、球壳状(纵坐标为粒子分布概率或密度,横坐标为速度)的分布)。
当粒子随流体由上游流至下游时,站在粒子整体运动的同心圆心上看到了扑面而来的下游流体和湍动元,与粒子速度圆心的相向运动速度就是delta_U,这时,粒子主要感受到的是head-on collision, 得到一次一阶fermi加速。随后粒子还将与各湍动元发生多次弹性碰撞,投掷角就被散开。这些与湍动元的碰撞产生了两个物理后果。一是,粒子得到加速,二是加速后粒子的速度分布被打成以下游速度为圆心的同心圆(圆的半径较刚才在上游时略变大)。后者是正确理解DSA过程的关键所在。这些粒子于是以新的同心速度分布(不同的速度分布圆心)随下游流体一起运动。总有部分粒子会重返上游,跨越波面时,这些粒子的整体运动信息是以下游速度运动的同心圆,站在圆心上,看到的依然是以速度delta_U扑面而来的上游流体和湍动,故类似的一阶加速同样在粒子由下游向上游的穿越过程中发生(加速与各向同性化isotropization)。可知,每次穿越激波面,粒子都是被一阶fermi加速的。如此反复,上下游的湍动就像在打乒乓球一样,把粒子加速到较高的能量(速度空间中的速度分布圆的半径变大)。直至湍动元无法约束高能粒子,粒子逃逸。
由于各向同性化的存在,这些粒子加速之后就忘记了自己初始的速度分布;因此,初始速度分布不是很重要;但初始能量大小却很重要,只有能量够高的粒子,才能被激波Fermi加速,这就是所谓的injection issue,why ? 同样是一个需要科普的问题。
稳态假设下,可求得DSA加速后粒子能谱的分布,为power-law,这与宇宙射线等高能粒子分布观测吻合,并且谱指数完全由激波压缩比决定。是一非常漂亮的理论。这一点,同样需要专门撰文科普。望有兴趣者阅读文献后,告诉大家究竟。请思考为何叫 Diffusive SA?
其实我了解亦很初步,此处勉力而为之,是为抛砖引玉,望同好协力为之,并敬请专家斧正,切切。
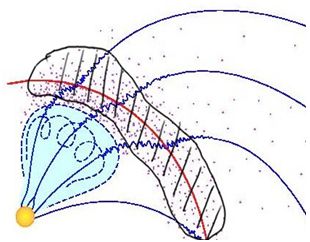
日冕物质抛射CME过程中CME在太阳风中的快速运动所驱动的激波结构(红线)和磁场位形、激波波前的湍动示意。
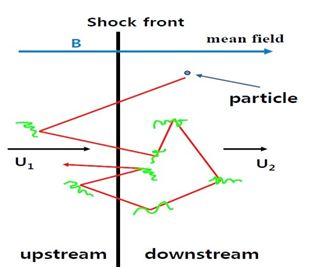
粒子与激波上下游湍动的碰撞(相互作用,散射)

激波坐标系中粒子穿越上下游时速度分布函数的变化(红色曲线)。红线转折点表示粒子穿越激波波面。
Plots under the shock rest frame
没有评论:
发表评论